SỬ DỤNG PHƯƠNG PHÁP TRUY HỒI ĐỂ GIẢI BÀI TOÁN ĐẾM

Biên soạn: Trần Hữu Hiếu

Bài toán: We want to cover the following 2 x 8 rectangle by using eight 2 x 1 rectangles.

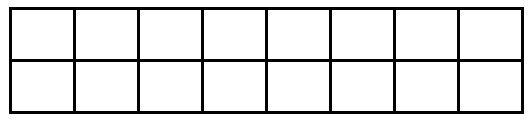
Each 2 x 1 rectangle is placed horizontally or vertically.

How many arrangements are possible to cover the 2 x 8 rectangle?

Dịch đề: Chúng ta muốn phủ kín lưới hình chữ nhật kích thước 2 x 8 bằng cách sử dụng 8 hình chữ nhật kích thước 2 x 1.

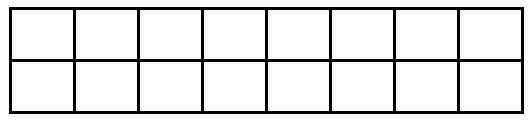
Mỗi hình chữ nhật chỉ được đặt thẳng đứng hoặc nằm ngang.

Hỏi có tất cả bao nhiêu cách sắp xếp để có thể phủ kín lưới hình chữ nhật 2 x 8 ở trên?

Phân tích:

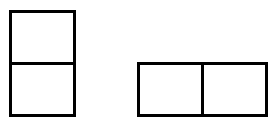
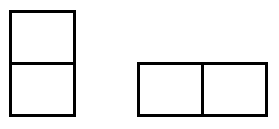
Khi tiếp cận bài toán này, thoạt đầu tiên, chúng ta thường thử một vài cách sắp xếp, và tất nhiên, chúng ta sẽ xuất phát từ các ô vuông bên trái. Ta thấy, ô vuông ở góc trên bên trái có thể được che phủ theo 1 trong 2 cách dưới đây:

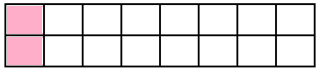
Cách 1:

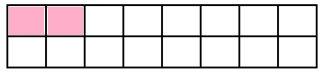
Cách 2:

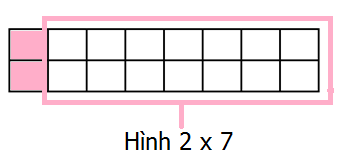
Với cách 1, ta nhận thấy số cách để phủ kín hình 2 x 8 lúc này chính là số cách để phủ kín hình 2 x 7.

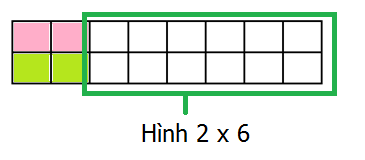
Với cách 2, ta thấy ô vuông góc dưới bên trái cũng được che phủ bởi 1 hình 2 x 1 đặt nằm ngang.

Phần còn lại chính là 1 hình chữ nhật 2 x 6.

Từ đó ta nghĩ đến việc đi xây dựng cách giải dựa vào việc xây dựng công thức truy hồi để tính số cách che phủ một hình chữ nhật có kích thước 2 x n, trong đó n là số tự nhiên lớn hơn 0.

Lời giải:

Gọi A_k là số cách dùng k hình chữ nhật kích thước 2 x 1 để phủ kín hình chữ nhật 2 x k. (với k là số tự nhiên lớn hơn hoặc bằng 2).

Dễ thấy:

A₁ = 1;

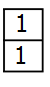
A₂ = 2;

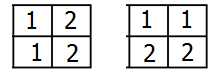
A₃ = 3

Xét hình chữ nhật kích thước 2 x n (n  3)

Xét ô vuông góc trên bên trái của hình 2 x n, ta có 2 khả năng sau:

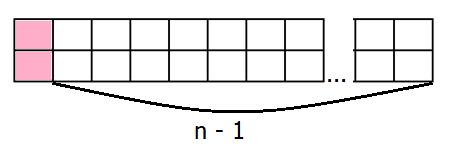
TH1: Ô vuông góc trên bên trái được che bởi hình 2 x 1 đặt thẳng đứng. Khi đó phần còn lại chính là hình 2 x (n – 1)                                                                                              (1)

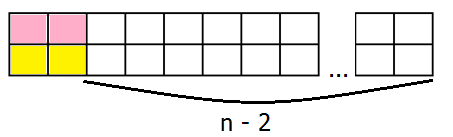
TH2: Ô vuông góc trên bên trái được che bởi hình 2 x 1 nằm ngang, khi đó ô vuông góc dưới bên trái cũng được che bởi hình 2 x 1 nằm ngang. Khi đó phần còn lại chính là hình 2 x (n – 2)   (2)

Từ (1) và (2) ta xây dựng được công thức truy hồi như sau:

            A_n = A_{n – 1} + A_n-2

Từ đó dễ dàng tính viết dược dãy A_n chính là dãy: 1; 2; 3; 5; 8; 13; 21; 34

Đáp án: A₈ = 34

Một số bài toán tương tự:

Bài 1. Có bao nhiêu dãy số gồm toàn các chữ số 1 và 2 và có tổng các số hạng  bằng 15.

Bài 2. Có bao nhiêu số có 8 chữ số, được tạo thành từ các chữ số 1, 2, 3 sao cho không có hai chữ số 1 nào đứng liền nhau.

Bài 3. Có một cầu thang gồm n bậc. Mỗi bước đi có thể bước lên 1 bậc hoặc bước lên 2 bậc. Tìm số các để đi đến bậc thứ n?

Bài 4. a) Cho hình như hình vẽ. Có bao nhiêu cách tô màu các hình tròn bằng 3 màu khác nhau sao cho 2 hình tròn bất kỳ được nối bởi 1 cạnh có màu khác nhau.

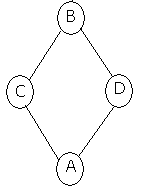
b) Có bao nhiêu cách tô màu 5 đỉnh của hình ngũ giác bằng 3 màu sao cho hai đỉnh được nối với nhau bởi 1 cạnh của ngũ giác thì khác màu nhau.

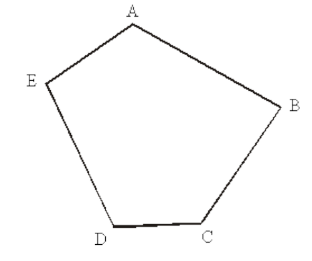
Bài 5. Gọi S_n là số cách tô màu n đỉnh của hình n-giác bằng 3 màu sao cho hai đỉnh được nối với nhau bằng 1 cạnh của đa giác thì khác màu nhau. . Hãy tìm công thức truy hồi để tính S_n.